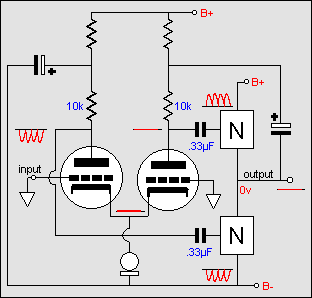
We begin by making the common cathode resistor infinitely large. In other words, if it is infinitely large, we can ignore the cathode resistor. As both triodes share the same rp , mu, and plate resistor values, we should expect that they would also share the same output impedances. And two equal impedance in series define a voltage divider that halves any signal. So if the first grid sees a +2 volt input signal, the first cathode will only be able to follow half way and thus see a +1 volt signal. Being grounded, the second grid sees 0 volts, but the second cathode sees the same +1 that the first cathode see, as they are connected. Therefore, the first triode effectively sees its grid move up 1 volt, and the second triode effectively sees it grid move down -1 volt.
    So if the common cathode resistor were infinitely large in value, the gain would match (actually, they wouldn't, as no cathode follower has a gain of 1: an imbalance of 1/mu remains). If it is not, it decreases the voltage division and thus decreases the input signal the second triode receives. This explains where the name "long tail" came from; the larger (the longer) the common cathode resistor value, the less the imbalance. Of course, an infinitely large cathode resistor implies an infinite negative power supply voltage.
     The constant current source frees us from the need to provide an infinite voltage. Independent of the voltage across it, it draws a steady current. Making a constant current source out of pentodes, FETs, MOSFETs, and transistors is easier than with a triodes. In this application, the triode's chief advantage, rp, becomes a liability, particularly when high current is needed, as high current triodes, such as the 6BX7 or 5687, have very low plate resistances. Still, by using a large valued cathode resistor, the triode's effective rp can be greatly increased. For example, a 6SN7's rp is 8k and its mu is 20, which when combined with a 10k cathode resistor yields an effective rp of 218k. Put mathematically,
   rp´ = (mu + 1)Rk + rp.

Correcting the Long Tail Imbalance
    This last circuit holds the answer to a problem not yet mentioned: the inequality of gain from each leg of the long-tail phase splitter. In a nutshell, the first triode realizes more gain than the second triode, which requires using a larger valued plate resistor for the second triode.
    Why is there an imbalance? The quick answer is that the common cathode resistor is not infinite in value. The longer answer is that long-tail phase splitter must present an equal drive voltage to each triode in order to develop an equal output gain. But as the first triode's grid sees all of the input signal and as the second grid only sees ground, how is this condition attainable? First of all, the input grid does not see all of the signal.
     If we look at the first triode carefully we see that it works as both a cathode follower and a grounded-cathode amplifier. Of course, if the cathode followed the grid perfectly, there would be no grid-to-cathode voltage variation, and thus no variation in current conduction, and thus no extra gain at the plate. However, the load that the cathode works into is not just the common cathode resistor, but that resistor in parallel with output impedance of the second triode. In other words,  we have a cathode follower that works into another cathode follower's output.

< PREVIOUS

NEXT >