Now lets place two equal valued resistors in series with each other across the power supply rails. At the center point, the noise cancels, as +1 added to -1 equals 0.

resistor. This voltage is in anti-phase with the power supply noise at the top rail, so it must be added negatively to the top rails noise voltage to determine the output noise.
            Vnoise(1 - Ra / 2Rk) = Vout
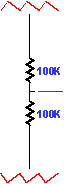
Notice that if Ra equals 2Rk the noise will completely null  out at the output. Unfortunately, the only way this condition can be fulfilled is if the grid-to-plate voltage is zero volts. Since the tube needs at least 50 volts to function, it seems that we will always have some power supply noise making itself known at the output. Two solutions present themselves. The first is to do what we have done here: add a voltage divider from plate to negative supply rail. This divider not only splits the level of the output signal, it splits the level of noise present on the plate and on the negative power supply rail.
   The first step to determining voltage divider resistor values is to establish how much noise is present on the plate. Plugging the Ra and Rk values into the above formula yields the following result: Vnoise (1 - 20K / 2•20K) = ½Vnoise. The next step is to find the null point between the plate noise and negative rail noise:
     ½ Vnoise / ( ½ Vnoise + Vnoise) = 0.333
In this case the answer is one third, which means the voltage division must be two thirds or 66%. We arbitrarily set the first resistor's value to 100K, a value not large enough to contribute excessive noise and not small enough to load down our differential amplifier. Setting the second resistor's value is easy as making it twice the value of the first resistor will result in the desired 66% voltage division.

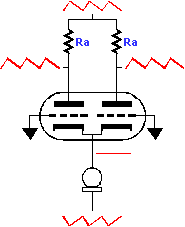
  Now let us review what happens in a Differential amplifier. If the common cathode resistor is replaced with a current source, or as it is also called, a current regulator, then the current flowing through the plate resistors will remain constant, which means that whatever voltage signal present at one end of the resistors must be also present at the other end or there would not be a constant voltage across the resistors. Paradoxically, current sources are generally thought to reduce noise, but they here work to realize all the noise on the top power supply rail at the output.

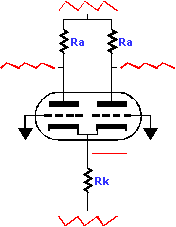
  Now let us replace the current source with a resistor. The resistor  is terminated by the cathodes to a near ground level amount of noise and at the other end it meets all the negative power supply rail voltage fluctuations. This configuration results in a fluctuation in the current flowing though the resistor and ultimately through the tubes and their plate

resistors, which are connected to the positive power supply rail voltage fluctuations. The net result is the positive rail noise is mixed with negative power supply noise, or rather, with anti-noise. To figure out the resulting noise at the output requires first recording the amount of AC noise voltage on one rail and then finding the current flow through Rk by dividing the voltage by Rk. Then this current is divided by two and multiplied against the value of Ra, which will yeild the amount of noise voltage developed across this

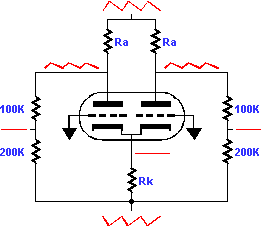
  The second approach to nulling the noise at the output is to accept our Ra and Rk resistor values and double the amount of power supply noise at the negative rail! For if the noise at this rail were twice the amplitude of the positive rail, the amount of noise induced current variation flowing through Rk would then be sufficient to completely null the noise at the plates. But how? Halving the value of the negative half of the power supply would be a good start. Still some

pg. 8

< PREVIOUS

NEXT >