|
|
infinitely high frequencies, the capacitor would serve as a dead short. In the first case the insertion loss would be zero and in the second case the loss would be equal to the voltage division between the two resistors. At some frequency in between DC and infinitely high frequencies, the reactance of the capacitor will equal the resistance of R2 and this frequency is F2. At some lower frequency than F2, the reactance of the capacitor will equal the sum of the two resistances, R1 and R2, and this frequency is F1. If the we set the ratio between the resistors to 50%, the bass boost will cover one octave; if ratio is set 25%, two octaves; 12.5%, three octaves.
How much feedback can be used?
In general, there is limited amount of feedback that can be applied to any transformer coupled amplifier, due to the transformer's complex, multiple poles at high frequencies that result in excessive phase shift. But at low frequencies, the transformer's transfer function should be a much simpler, single-pole, high-pass filter action, as the low frequency cutoff is determined primarily by the shortage of inductance from the transformer. All of which means that more feedback can be applied at the lower frequencies than the higher frequencies. And as our design goal was little, if indeed any, feedback at mid and higher frequencies, the usual stability problems associated with feedback should not present themselves here. Still, a sane limit might be 30 dB of feedback at the lowest frequencies.
Where should F1 and F2 fall?
Because the transformer contributes its own low frequency cutoff point, F1 will have to fall at or above this frequency. F2 is set by moving n octaves away from F1 based on how much feedback we wish to apply to the low frequencies. For example, assuming that a transformer had sufficient low frequency bandwidth to set F1 at 25 Hz and we set 12 dB as the limit to feedback to be applied, F2 would fall at 100 Hz. The math behind this is:
F2 = F1·10(feedback in dB)/20
or F2 = F1·(open-loop gain / closed-loop gain)
or F2 = F1·(R1 / R2 + 1).
The best design procedure is to measure the open-loop gain of the amplifier first and then decide how much sensitivity is required. For example, given an open-loop gain of 100 and a maximum output RMS wattage of 16 watts into 8 ohms, we might decide that we want the sensitivity of the amplifier to equal one volt at the input for full output. Now we must decode the output wattage into peak volts:
V = Ö(Watts·2·Restance).
We now divide the peak output voltage by 1 volt and we
|
|
|
|
|
arrive at the desired gain. This figure is then divided into the actual open-loop gain of the amplifier, which must be greater or this design trick will not work. For example, if the result is 4:1, then we can realize 12 dB of feedback at the lowest frequencies, as
20·Log(ratio) = feedback ratio in dB.
The next step is to detremine the values of R1 and R2. The value of R2 is abitrarily choosen first (let's say, between 1k and 100k). Second,
R1 = (ratio - 1)·R2.
For example, if we set the value of R2 to 20 kohm, then R1 equals (4 - 1)·20,000, or 60 kohm. The last step is to decide on a value for the capacitor that connects to R2. Our feedback ratio sets the number of octaves between F1 and F2, but not the actual frequency of either, at least one frequency must be choosen. If 30 Hz was choosen for F1, then F2 would be 120 Hz, as it is equal to ratio·F1. Conversely, if we choose 100 Hz for F2, F1 would be 25 Hz, it is equal to F2 / ratio. Once the values for F1 and F2 are known, the capacitor's value can be fixed easily:
capacitor = 1 / (6.28·R2·F2).
(or to preformat the capacitor's value in µF)
capacitor = 159155 / R2 / F2.
Putting it altogether
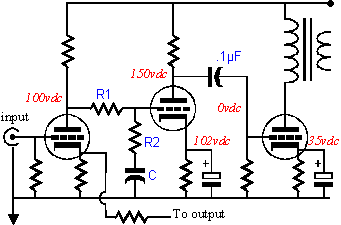
Once the values for the shelving network have been figured out, the question remains: Where should it go? It cannot be placed before the amplifier, as the feedback will serve to maintain the skewed frequency response of the network. Probably the best place for it is in between the first stage and the second, providing that the feedback loop extends to the first stage. A single-ended amplifier might be configured as the schematic below.
|
|
|