1st Order Filters
    Simplicity itself: a resistor and a capacitor in between two cathode followers. We can eliminate some the components in the signal path but at the cost of eliminating some its universality. The circuit below makes the point.

2nd Order Filters
    The 2nd and higher order filters rely on the cathode follower to provide positive feedback at some frequencies to define the desired crossover shape. In the highpass filter below, resistor R1 provides the positive feedback path back into the circuit.

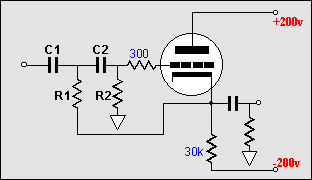
    The deviation between resistors R1 and R2 and the "nominal" resistor values defines the Q of the filter. The nominal value is the textbook (R = 1/(2piFC) value. For example, given a crossover frequency of 1 kHz and a capacitor C1 value of .159µF, the nominal resistor value is 1k. In a Butterworth filter, R1's value would be 707 ohms; R2, 1414 ohms. The Butterworth filter uses 1/Ö2 and Ö2 to achieve its alignment. Thus the ratio between R1 and R2 is 2.
    The Bessel filter uses a more complicated ratio: R1 = 3/4xR2. R2 is twice the nominal value and R1 is 75% of R2's value. At the core of these relationships is Ö3. For example, (Ö3 /2)² = 3/4. Fortunately, once one set of resistor and capacitor values have been determined, setting a different crossover frequency only requires scaling either (but not both) the resistor or the capacitor values up or down.
    (Q is the inverse of the damping factor of a filter. Thus a Q of .5 equals a damping of factor of 2. Thus the higher the Q, the less damped the filter is and the more likely it is to ring or peak. The lower the Q, the more likely the output will droop at the crossover frequency. Expect to see both Q and "damping" used in the literature.)

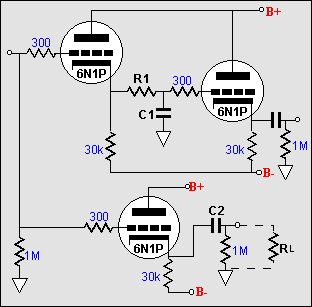
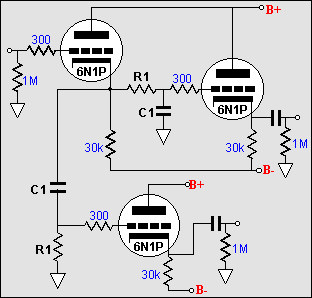
    The low pass filter is safely tucked inside the two cathode followers and the highpass filter is buffered from the output impedance of the signal source; but its termination is can change with a different power amplifier. Consequently, a better choice might be to enclose the high pass filter within the confines of the two cathode followers.

< PREVIOUS

NEXT >