|
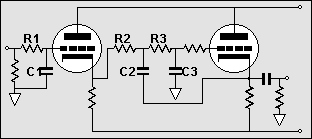
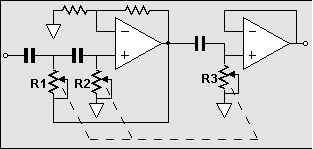
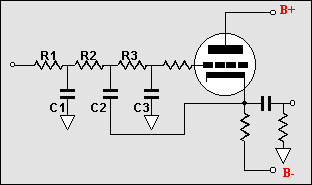
3rd Order Filters |
|
What advantage does one hold over the other? For the cathode follower based filters, little advantage exist other than the two section method having one less active device in the signal path. But if the buffers were replaced with amplifiers, then the two section method allows for all the resistors to equal each other. How is that an advantage? If all the resistors equal, then an adjustable crossover point can easily be had by using a three deck potentiometer to set the crossover frequency. |
|
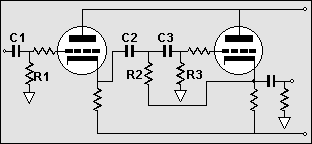
4th Order Filters |
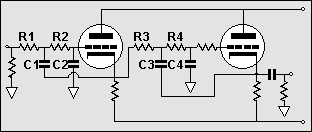
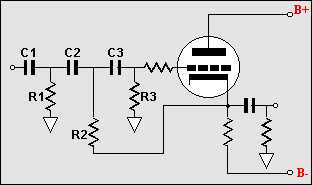
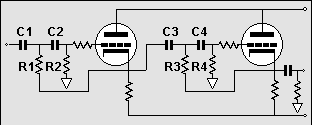
|
|
||
Pg.
5