air-gapped. Normally, an inductor must have an air-gapped core to withstand the magnetizing influence of the direct current flowing through the inductor's winding. But if two identical windings are used and these windings give rise to opposing magnetic fields, then the result is that the inductor never experiences a net polarization of its core. Consequently, a tight magnetic circuit, such as occurs in a toroidal core can be used without fear of saturating the inductor.
   This type of inductor bucks changes in current flow just as a nor inductor does, but does so in a bipolar fashion. The degree to which the two power supply rails draw an equal current flow is the degree to which this type of inductor is suitable to the task. In those cases where the rails do not see an equal current draw, using two separate air-gapped inductors is the best approach.
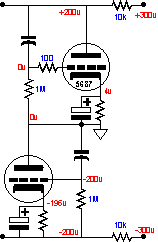
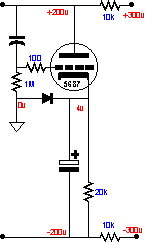
    Now, if we can transfer the principles of operation from the previous example over to the shunt regulator model, we will understand how two types of shunt regulators can be matched to two different power supply scenarios.
    If the power supply rails see differing current demands, then two separate shunt regulators should be used. Each takes care of its own rail voltage. Each is referenced to ground. And each requires its own support circuitry and probably its own heater power supply. (Most tubes indirectly heated tubes have about a 100 volt limit on the voltage difference that can exist between cathode and heater. Remember, there is only a few molecules separating these two elements.) 
  On the other hand, if the power supply rails see equal current demands, then one  shunt regulator should be used, as it takes care of both rail voltages, being referenced to not to ground, but to the other rail. And it

is unlikely to require its own support heater power supply, as the cathode is within a few volts of ground potential. 

  The effectiveness of the dual shunt regulator configuration is given by following formula:   
     Noise Reduction = muR / (R + rp),
given a mu=20, a R=10k, and a rp=2.5k,
     16 = 20x10000 / (10000 + 2500).
   The effectiveness of the single bipolar shunt regulator is given by following formula:   
     Noise Reduction = 4muR / (2R + rp),
given a mu=20, a R=10k, and a rp=2.5k,
     35.5 = 20x2x10000 / (2x10000 + 2500).
Thus, the single bipolar shunt regulator is twice as effective than the dual regulator version. Why? The dual version only sees its own power supply rail noise, whereas, the single bipolar version sees the noise from both rails added together. Furthermore, the effective value of the series resistor is doubled, which improves performance somewhat. But we can further slant the scale in favor of the bipolar version by pointing out that since two triodes were needed to make a dual version, those two triodes could be paralleled up in the bipolar version, doubling again its effectiveness.
                          Editor

<PREVIOUS

pg. 19

NEXT >