Improved Crossover Design
An entirely different topic was to fill this post, but the topic of making better loudspeakers won't let my mind break free. A few weeks ago, I explained to a friend my preference for the series crossover over the equivalent parallel crossover topology, wherein I detailed how the impedance loading the loudspeaker drivers see outside their portion of the audio bandwidth was far lower with the series crossover. A few days later, I realized that my argument assumed that the woofers, midranges, and tweeters all shared the same efficiency (SPL per 2.83V at one meter). Before I get ahead of myself, we must first understand how a series crossover differs from a parallel crossover.

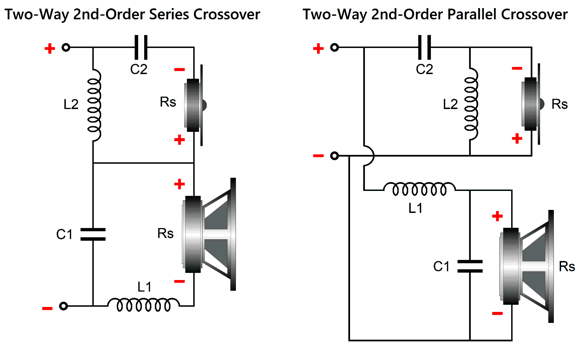
The parallel topology is what most audio practitioners know and what most loudspeaker enclosures contain. (If your speaker offers bi-wire connections, it certainly holds a parallel crossover.) Both topologies deliver the same results in SPICE simulations, where the loudspeaker drivers are conveniently and confidently replaced by 8-ohm resistors. Real loudspeaker drivers, alas, are nothing like 8-ohm resistors, being instead complicated mechanical-electrodynamic devices. For example, with the exception of planar electrodynamic drivers, few loudspeaker drivers actual deliver a DCR of 8 ohms, delivering instead a rollercoaster plotline of impedance versus frequency. Does this matter? Indeed, it does.

From my Post 481, this in turn quotes my Post 402:

About 30 years ago, I got a phone call out of nowhere from a retired Ph.D. in electrical engineering, who had spent his working life devoted to electronic filter design. He had heard of my (unearned) reputation as a crossover wizard and he wanted to get together to talk crossovers. During our conversation, I learned that he had always been concerned with loudspeaker crossovers and now that he was doing freelance design consultations for speaker companies, mostly pro-audio types, he was being paid to develop better crossovers. He had tried scores of designs and alignments, but after years, if not decades, of experimentation, nothing had beaten the first-order, series crossover. It alone delivered the sonic goods. The problem was, of course, that all 1st-order crossovers made huge demands on the loudspeaker drivers to provide wide bandwidth and they offered little protection to delicate tweeters, particularly those in pro-audio applications.

I asked him why the series arrangement bested the far more common parallel arrangement. Here was his answer, which I detailed in  Post 402 .

"His theory was two-part: first, any crossover order higher than the first must give rise to phase aberrations; and, second, by shunting the loudspeaker drivers with capacitors and inductors in the series crossover the drivers see needed dampening where they needed it most, i.e. outside their bandwidth limits. In other words, the woofer gets shunted by the capacitor's falling impedance as the frequency extends beyond its high-frequency range, just as the tweeter gets shunted by the inductor's falling impedance at the tweeter's resonant frequency. In contrast, he argued, in the parallel crossover, the woofer becomes unloaded at high-frequencies, as the inductor's increasing impedance decouples the woofer from the amplifier's low output impedance. (Goodbye damping factor of 2,000.) And the tweeter finds no useful damping resistance at its resonant frequency, as the crossover capacitor's impedance has climbed to too high a value to prove useful."

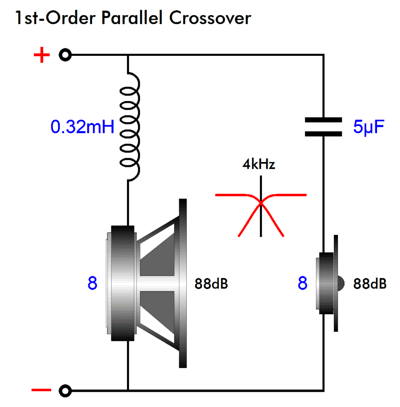
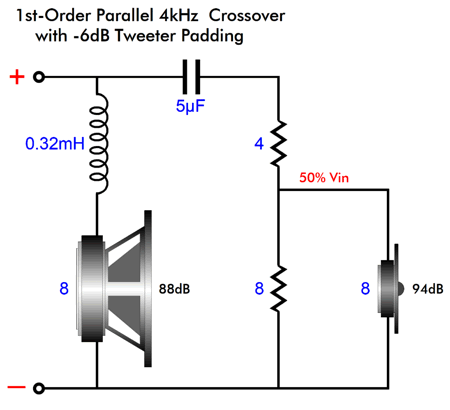
I have covered the problem of tweeter resonance in my Post 590, in the section titled "Important Caveat About Fs."

Here SPICE simulations do prove useful. Let's start with a simple 1st-order parallel 4kHz crossover.

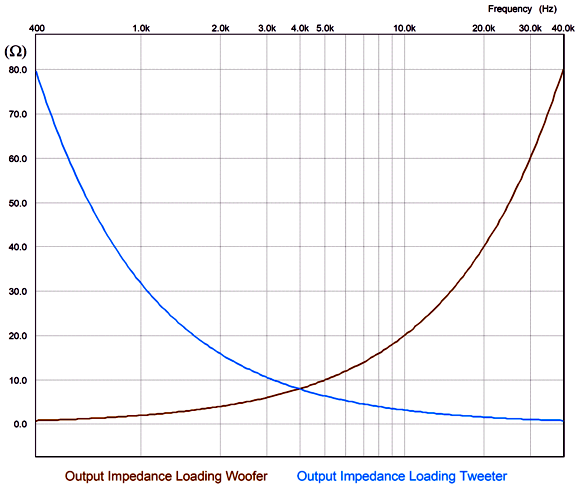
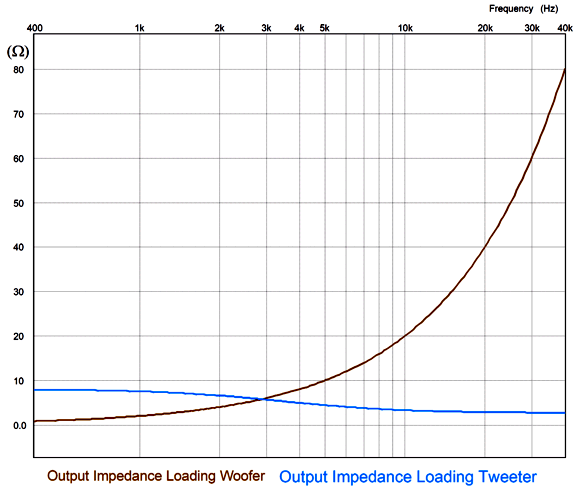
We use the same capacitor and inductor values to make a series crossover, which will perform in a perfectly-equal fashion in SPICE simulation with resistors replacing real loudspeaker drivers. The problem is those resistors do not care what the source impedance is of the electronic device powering them. A resistor experiences the same voltage drop and dissipation no matter what the source impedance is. Here is the SPICE-generated impedance plotlines created by the parallel crossover topology.

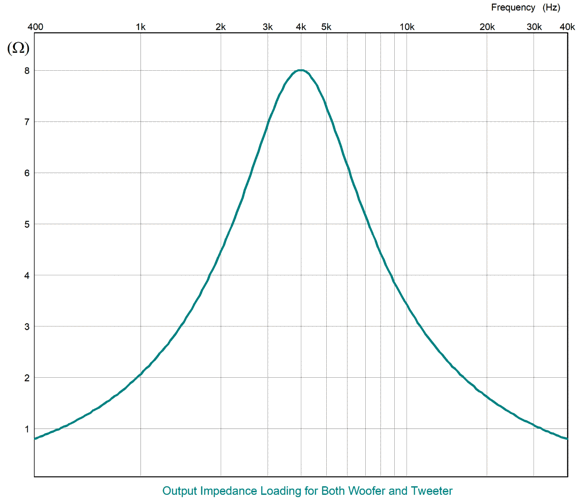
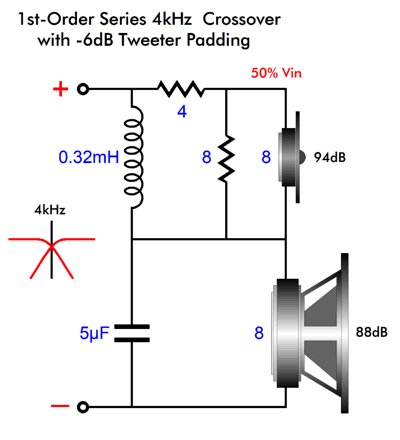
At the crossover frequency, both the woofer and tweeter see the same 8-ohm source impedance (assuming vanishingly-small output impedance from the power amplifier). At DC, the tweeter sees an infinitely-high source impedance, while the woofer sees zero ohms of impedance, but infinitely high frequencies it, too, sees an infinitely-high source impedance. Consider this: what if much of the sonic benefit resulting bi-amping results not from doing away with the passive crossover part imperfections, but their source impedance, as a good power amplifier delivers both a low and flat output impedance across the audio bandwidth. Let's compare the previous graph to the following graph for the series crossover.

Once again, at the crossover frequency and only at the crossover frequency, both the woofer and tweeter see the same 8-ohm source impedance. At DC, the tweeter and woofer both see zero ohms of impedance, while at infinitely high frequencies both see the same zero-ohm source impedance.

Does this matter? Oh yes, indeed it does. For example, the highly esteemed dome tweeter from Scan-Speak, the R3004/602200 Illuminator Ring Radiator Tweeter, exhibits a resonant frequency of 430Hz, with a mechanical Q (Qms) of 2.3, an electrical Q (Qes) of 0.48, and a total Q (Qts) of 0.4, which is derived from placing the Qms in parallel with the Qes.

With the parallel crossover presenting an impedance of 78 ohms at 430Hz, the tweeter's Qes rises to 12.96, while its Qts climbs to 1.88. Now, a Qts of 0.4 is nicely damped, but a Qts of 2.3 is exuberantly peaky, as it represents a peaking of 5.5dB. Let's compare this to the series crossover. It presents an impedance of 0.9 ohms at 430 Hz, which will cause the tweeter's Qes to rise to 0.62, and its Qts to rise to 0.49. (Critically damped is at a Q of 0.5.) Which do you think would sound better?

Here is another question: what's the point of having a power amplifier that delivers a damping factor of 400, when the crossover presents an impedance of 78 ohms at the tweeter's resonant frequency?

So far, the assumption has been that the woofer and tweeter share the same SPL sensitivity at 2.83V/Meter. Usually, woofers lag far behind midranges and tweeters; thus the need for L-pads to reduce the output from the higher-SPL drivers to match that of the low-efficiency woofer.

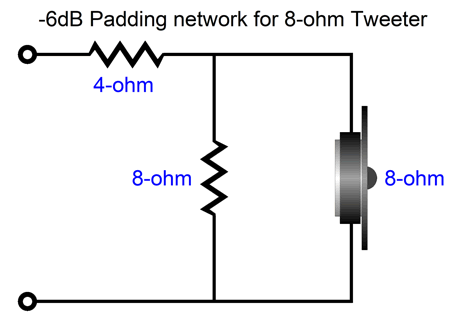
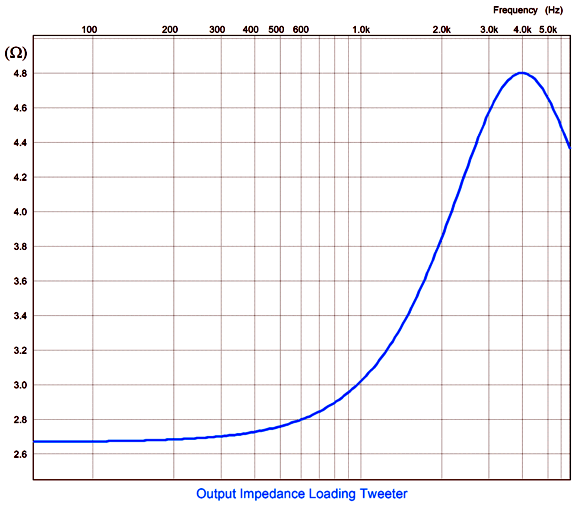
This example cuts the input voltage the tweeter in half, which results in a -6dB reduction in its SPL. As far as the crossover is concerned, the load is still 8 ohms. As far as the tweeter is concerned, the lowest source impedance it can ever see is 2.66… ohms, as 8 in parallel with 4 equals 2.666… Let's add this L-pad to the parallel crossover.

The woofer and tweeter now deliver the same SPL. The source-impedance plotlines look different now.

The tweeter now sees a high of 8 ohms and a low of 4 ohms. Certainly for the tweeter at resonance, 8-ohms is far better than 78 ohms, so we see the L-pad actually doing more than just attenuating. Next, we add the L-pad circuit to the series crossover.

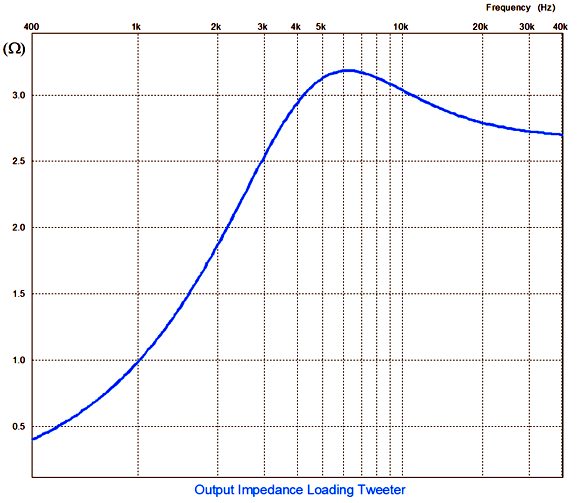
The resulting source-impedance plotline proves interesting.

Peaks at 4.8 ohms, with a low of 2.666… Better but not perfect. Okay, it's now time to reveal my workaround, i.e. my fix.

2nd-Order Crossovers
We will start with a standard 2nd-order Linkwitz-Riley 4kHz two-way crossover.

Next, we apply my fix:

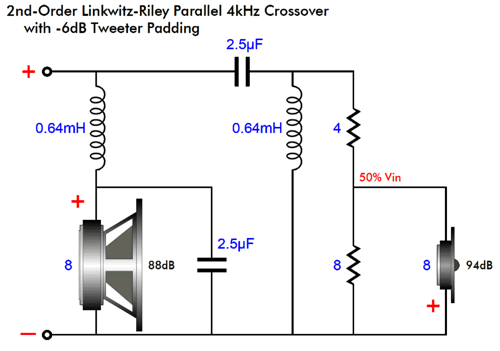
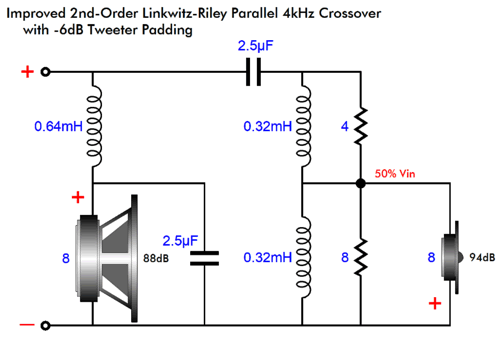
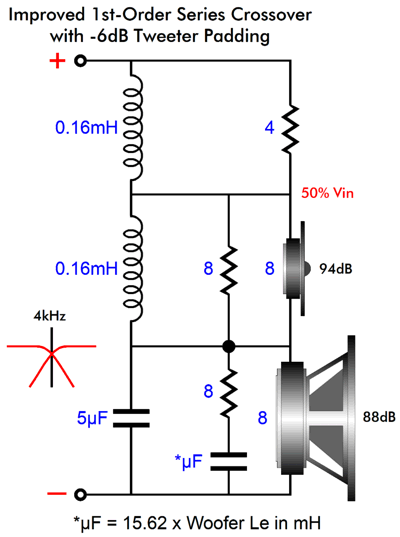
Note that both L-pad resistors get shunted by inductors, with half the inductance of the previous single inductance. The 8-ohm resistor in parallel with the tweeter's 8-ohm impedance creates an impedance of 4 ohms. In other words, the top and bottom resistances match, so it makes sense that each inductor presents half the inductance. (Bear in mind that inductances add when placed in series, just like resistances. In other words, the two inductance must add up to the original single inductance.)

What if the tweeter was attenuated more than -6dB, say -12dB? in this example, the top resistor would equal 6 ohms, while the bottom resistor would equal 2.666… ohms, with a 2.7-ohm resistor being close enough. The bottom 2.666-ohm resistor in parallel with the 8-ohm tweeter results in a 2-ohm resistance, making for only 25% of the input signal getting to the tweeter, thereby resulting in an attenuation of -12dB. In this setup, the top resistor would be shunted by 0.75 x 0.64mH (i.e. 4.8mH), while the bottom resistor would get an inductor equal to 0.25 x 0.64mH (i.e. 0.16mH). Note that without the L-pad resistors, the tweeter would encounter a dead short both at DC and at infinitely high frequencies. With the two resistors and two inductors, the same dead short occurs at DC; but at infinitely high frequencies, the source impedance levels out to 2.666 ohms.

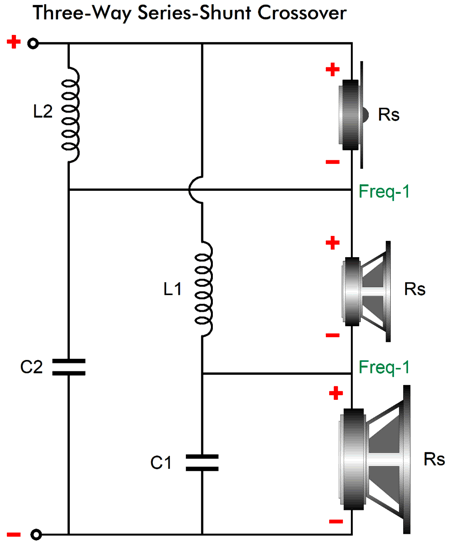
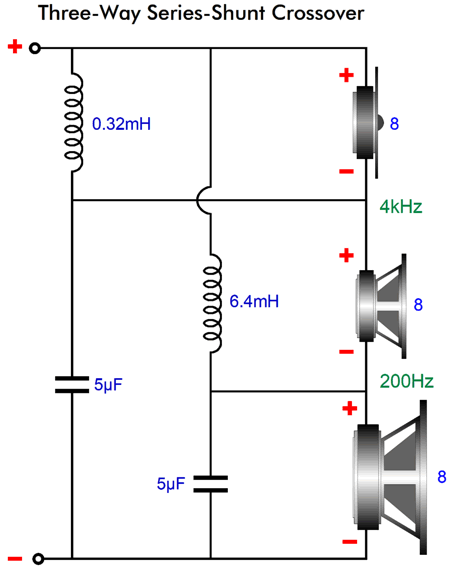
Series-Shunt Crossover
Let's return to my favorite crossover topology, the series, and apply my fix.

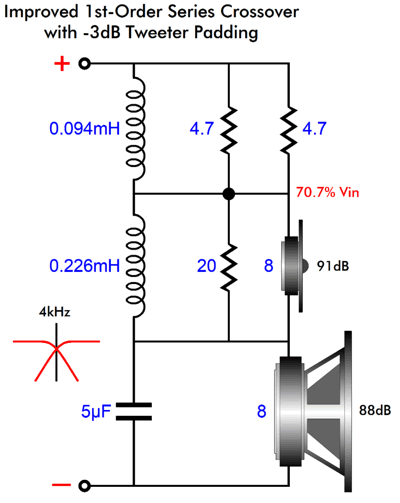
We see the same 50% attenuation of the tweeter's signal and the same equal division of the inductor values. (I added the Zobel network across the woofer, as the woofer voicecoil's inductance will trip up the crossover's functioning. Okay, now let's look at the same crossover but with a -3dB L-pad.

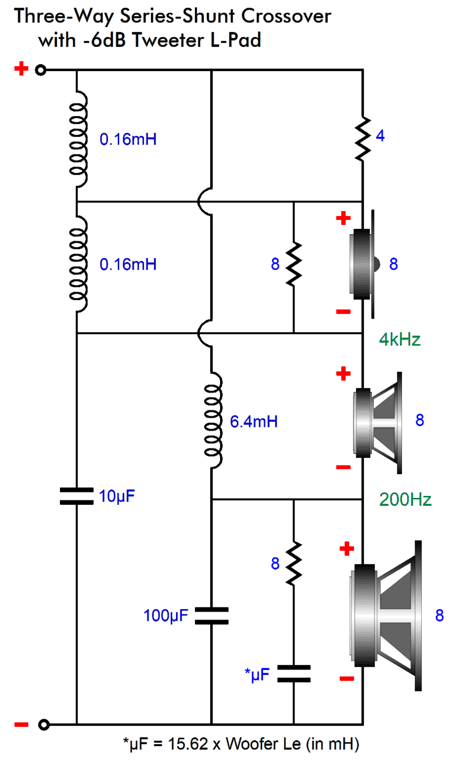
If you do the math, you will see that the two inductor values match the two resistances ratio. In addition, 0.094mH added to 0.226mH equals 0.32mH. Basically, wherever we find a tweeter shunted by an inductor and attenuated by an L-pad, we can apply my fix; for example, the series-shunt crossover topology.

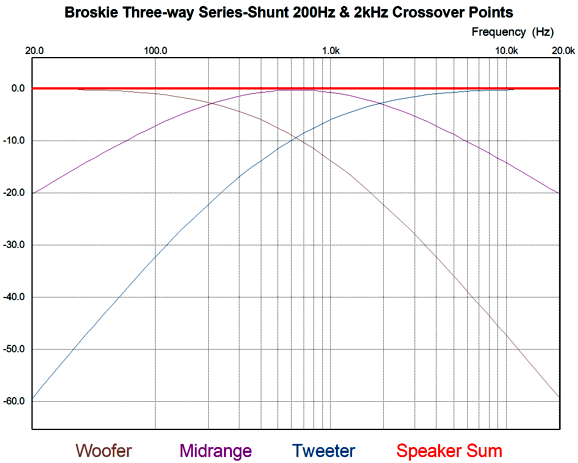
Like the 1st-order crossover, this topology offers a flat frequency response with a voltage-out power amplifier (which 99.9999% of amplifiers are) and a flat phase. It differs, however, in exhibiting a slight dip in impedance in the mid frequencies. Unlike the 1st-order three-way, which can deliver either a cascaded woofer or a tweeter cut-off slopes but not both at once, this topology produces the cascaded slopes for both the woofer and tweeter. In other words, the woofer and tweeter slopes start off as -6dB per octave and then increase to -12dB per octave, which offers greater protection for the delicate tweeter voicecoil and gets the sluggish woofer out the way before it can muddy up the midrange.

Next, ere is a design example with 200Hz and 4kHz crossover frequencies. Note that the tweeter is shunted by an inductor, which means that if the tweeter needs an L-pad, we can the two-inductor fix.

Once again, a -6dB L-pad is shown, just to make the math easier.

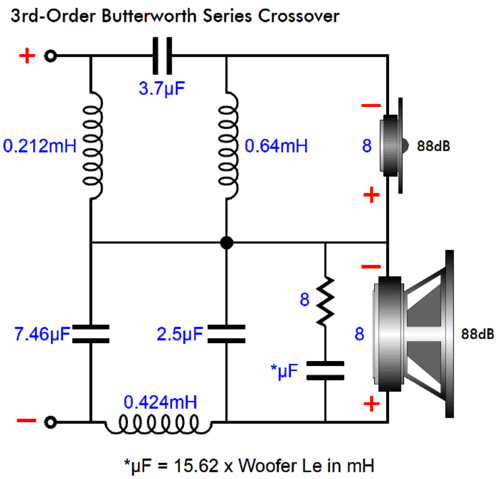
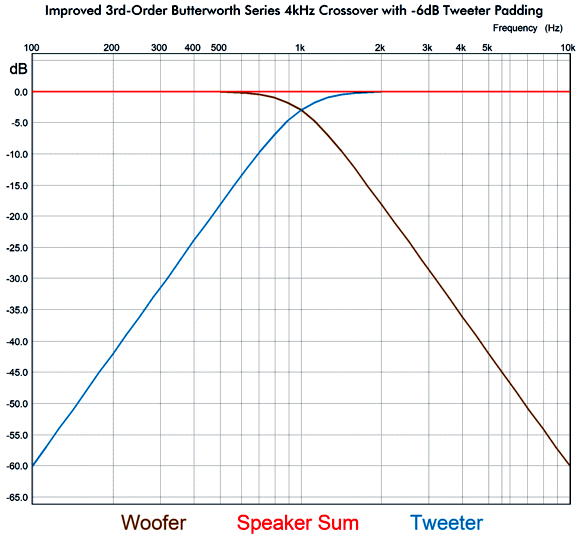
3rd-Order Crossovers
Another crossover topology that shunts the tweeter with an inductor is the series 3rd-order crossover.

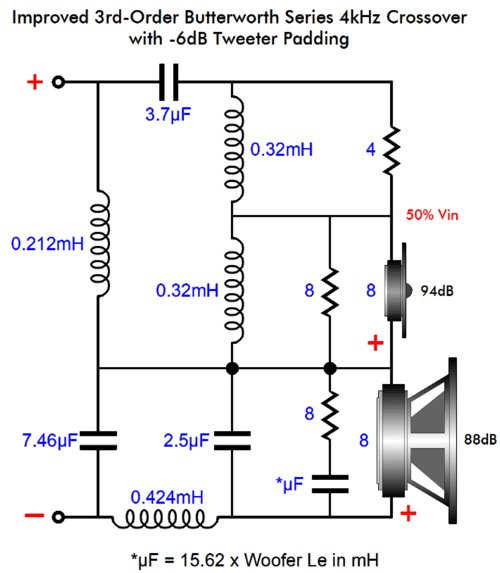
We will add a -6dB L-pad and two-inductor fix.

Just to make sure that this setup actually works, I ran the circuit in SPICE simulations and got this result:

Textbook perfect. What about 4th-order crossovers?

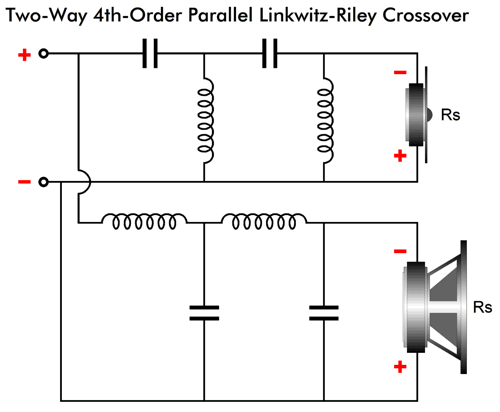
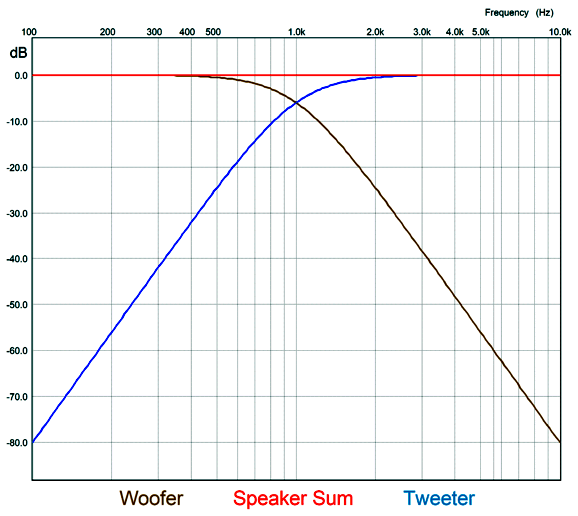
4th-Order Crossovers
Much like the 2nd-order Linkwitz-Riley parallel topology, the 4th-order Linkwitz-Riley parallel crossover also shunts the tweeter with an inductor.

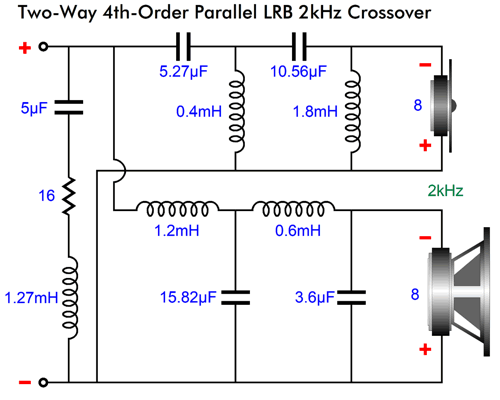
Like the 2nd-order Linkwitz-Riley parallel topology, the 4th-order Linkwitz-Riley parallel crossover puts both drivers -6dB down at the crossover frequency; but unlike the 2nd-order, the 4th-order Linkwitz-Riley parallel crossover requires that both woofer and tweeter are wired in phase to each other. The 4th-order slopes are steep and offer extreme tweeter protection. I once heard a homemade loudspeaker that used this crossover with a 7-inch woofer and 1-inch dome tweeter that sounded amazing—in spite of playing inside a huge room at high SPLs. (If I remember correctly, the crossover frequency was 2.2kHz. far below the usual 3kHz crossover frequency.)

To be down -80dB one decade away from the crossover frequency means an attenuation of 1/10000. For example, a 100W power amplifier puts out 40Vpk into an 8-ohm load, so -80dB attenuation equals 4mVpk of signal. In contrast, the 1st-order yields only -20dB of attenuation; thus, 4Vpk of signal; the 2nd-order, 0.4Vpk; the 3rd-order, 40mVpk.

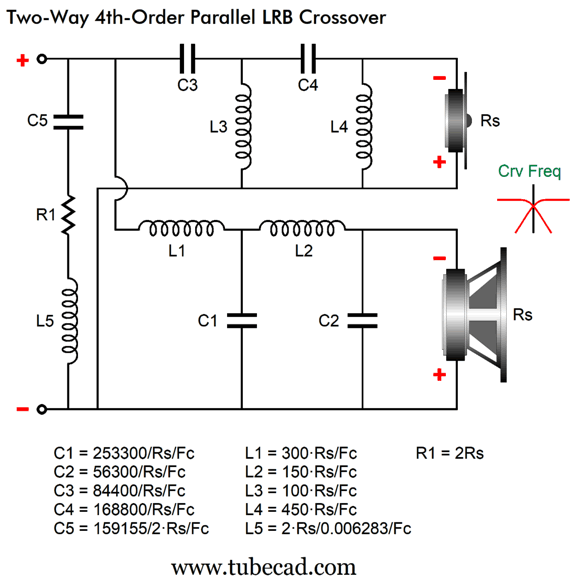
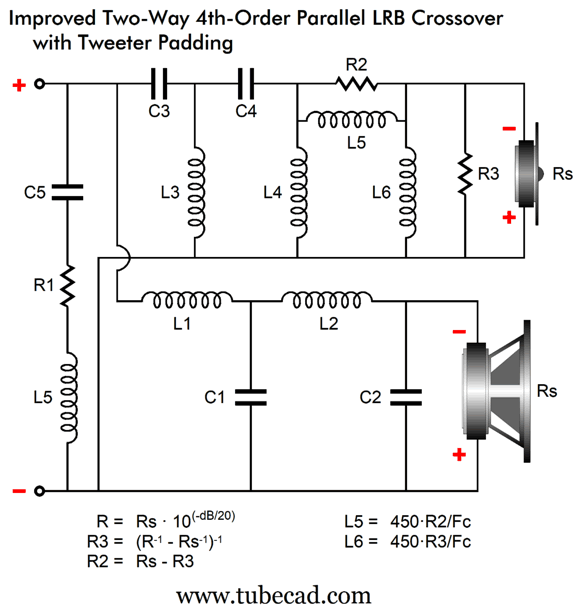
Parts C5, L5, and R1 are my contributions to flatten the impedance plotline, which would otherwise spike up at the crossover frequency. Here is a design example at 2kHz.

Adding an L-pad two-inductor fix is easy.

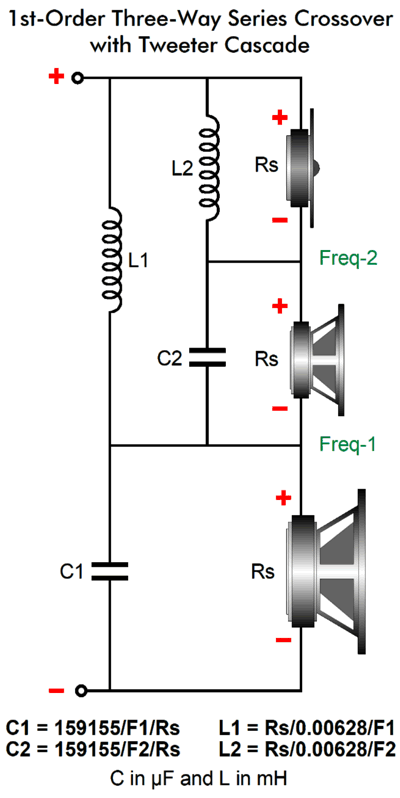
Capacitor L-Pad Fix
Okay, now that the dead horse is thoroughly beaten, we can move on to dealing with drivers that are shunted by capacitors. Most woofers exhibit such high intrinsic inductance (Le) that the shunting capacitor's decreasing impedance with higher frequency little matters; in addition, it is rare, extremely rare, to ever use an L-pad on a woofer. On the other hand, because the woofer's inductance is so high, it can easily throw off the crossover's functioning in a series crossover; thus we should always add a Zobel network to undo the inductance.

Midranges, on the other hand, present much less voicecoil inductance (ribbon and planar midranges usually present next to zero inductance) and often deliver higher SPL than the woofer. In other words, they do get L-pads, so we can apply my two-capacitor fix. Here is a three-way 1st-order crossover that I truly like, as the crossover's tweeter cascading slopes offer greater protection and still delivers a flat phase response. In other words, a square wave goes in and a square wave comes out—well, it comes out more like a square wave than 2nd-order or 3rd-order or 4th-order crossovers can ever hope to produce.

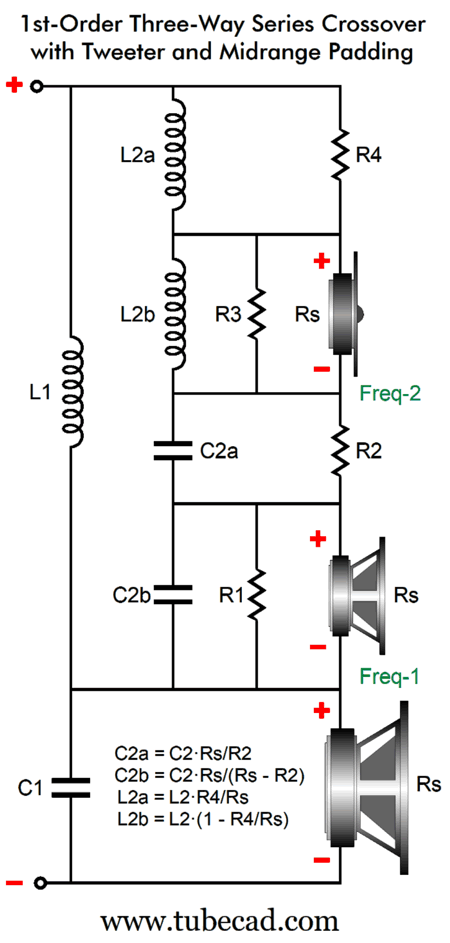
The required math is mercifully easy.

Both the midrange and tweeter get L-pads, which can differ in attenuation. A typical SPL disparity is along the lines of the tweeter delivering 96dB, the midrange 91dB, and the woofer lagging behind at 88dB. Note that the single capacitor shunting the midrange has been replaced by two capacitors. Capacitors, unlike inductors and resistors, do not add in series; instead, like resistances in parallel, they subtract. For example, two 20µF capacitors in series yield only 10µF of capacitance. In other words, expect to use bigger capacitor values.

I began this section by quoting my earlier post, so I will end it by also quoting a previous post:

Fixing the Tweeter Fs Problem
Problem? What problem? Before spelling that problem out, let's just step back and consider why so many high-end loudspeakers hold obscenely complex passive crossovers, crossovers that bear little resemblance to textbook crossover circuits, looking more like a jigsaw puzzle forced together with a mallet by a blind man. Why the overly complicated and unfathomable crossovers? A flat frequency response—at any cost, such as the expense of forgoing a flat impedance plot or a flat phase response. This all-too-common situation reminds me of an old joke, which I first heard being described as a quintessential Southern joke.

A man walking past a store window beholds two miracles. The first is the finest men's suit he has ever beheld, made of unsurpassed cloth, with a crisply defined lapel that reposes perfectly around the neck, and made to the latest style. The second miracle was the price: only $100. He rushes in the store, and soon his fingers fondle the luxurious fabric, his eyes suck in the perfect, delicate stitching inside. He asks that the suit be taken down so that he might try it on. Standing before the three-sided mirror, he says, "It's absolutely superb, but the left arm is a lot longer than the right arm."

He is informed that no alteration can be made, as the cloth is so exquisitely fabricated that any cutting would provoke long runs through the material; but he is told that he only needs to cock his left shoulder up a little, while tucking the left lapel under his chin a bit, and stand slightly sideways, so the longer arm faces slightly forward. He performs the tasks, and he is dazzled by the transformation. He struts about the room in this fashion and, then, notices that the pants' right leg is far too short.

"That is not that big a problem," the store owner explains, "Just keep your right knee bent a little at all times, walk like this, and no one will notice. Yes, it takes a little work, but that’s why this suit is only $100, not $3,000."

He buys the suit and wears it out the store, cocking his left shoulder up, tucking the suit’s left lapel under his chin, twisting his torso, bending his right knee, and limping along the street. A couple notices him, and the wife blurts out, "Good heavens, isn't that our old high-school classmate, Jim Long? He was a star athlete, but look at him now, all crippled and deformed. Surely some terrible accident or disease must have happened to him."

Her husband stares and says. "Yes, it is surely a sad, sad sight, seeing him all misshapen, but doesn't that suit just fit him fine?

Returning to loudspeakers with misshapen passive crossovers, if woofers and tweeters were perfect, we would see simple, textbook passive crossovers used. Of course, the harsh reality is that all drivers fall short of perfection. Indeed, if a perfect loudspeaker driver existed, no crossover would be needed, as it would cover the entire range of audio frequencies from 20Hz to 20kHz by itself.

Often, I have been asked just what the whole point is behind my many, many posts. My answer is simply that I hope raise the general level of audio equipment. At the same time, I wanted to write and create content that be something that I would want to read and see, if I weren't mine. Well, this post will at first be largely ignored, but in about ten years I expect that my L-pad fix will simply be established practice in the making of loudspeaker crossovers. At first, only a few high-end loudspeaker makers who read my posts will quietly introduce the fix, but once their competitors take apart their loudspeakers to see what changed, the practice will spread.

Okay, I take that last sentence back. That's not how things work in the loudspeaker industry. Crossovers are designed in Crossover Software, just as the enclosure volume and port diameter and length are designed dictated by Speaker-Enclosure Software. Following the prescribed decisions of software is not only easy, it is safe. Safe in that if things do not turn out well, you are exempt from blame, as you were only following digital orders. When Vance Dickason releases his 15th Edition of The Loudspeaker Design Cookbook with my crossover fixes, the creators of crossover software will incorporate them the code.

Music Recommendation: Lucinda Williams' Tetralogy
Whenever discussing the blues and country American singer, songwriter, and guitarist, Lucinda Williams, it is a safe procedure to begin by pointing out that her singing voice is an acquired taste, which explains why, in spite of rave reviews, she is little known and has gotten little radio play. Born in 1953, Williams is still producing great albums. I first discovered her with her 2007 album, West; and then again with her singing on Charles Lloyd & The Marvels' album, Vanished Gardens. Recently, she released an album of The Beatles' covers, Lucinda Williams Sings The Beatles From Abbey Road, which makes it her fourth tribute album, with the previous three devoted to Bob Dylan, Tom Petty, and The Rolling Stones.

If you are under the age of sixty, you probably cannot understand how the culture and minds were heavily influenced by The Beatles. Each new song from the (original) Fab Four hit the earth like a meteor large enough to level London. Throughout the day, you would be asked, "Did you hear it?" To a lesser extent, the same holds true for The Rolling Stones, Bob Dylan; and to a much, much lesser extent, Tom Petty in the late 1980s. A singer must bring something special to a cover album of these treasured standards, something new and revelatory. Williams does.

//JRB

Did you enjoy my post? Do you want to see me make it to post 1,000? If so, think about supporting me at Patreon.

User Guides for GlassWare Software
Just click on any of the above images to download a PDF of the user guides.